Operaciones con funciones racionales.

Las operaciones con funciones racionales se realizan basados en las operaciones con fracciones y factorización, como se presenta a continuación.

Ejemplo 1. Simplificando una función. Simplificar la función racional $$f(x)=\frac{2x^2+3x-35}{x^3-19x+30}$$ Solución: aplicando la regla del trinomio \(ax^2+bx+c,\) y de Ruffini y se reescribe \(f(x)\) como, $$f(x)=\frac{(2x-7)(x+5)}{(x-3)(x-2)(x+5)}=\frac{2x-7}{(x-3)(x-2)}$$ Observación importante. Siempre conviene escribir la respuesta factorizada, esto ofrece la oportunidad de observar si el numerador posee o no algún factor con el denominador que puede ser simplificado, como en este caso no lo hay se puede desarrollar el denominador (si se desea) y así escribir, $$f(x)=\frac{2x-7}{x^2-5x+6}$$ Ejemplo 2. Denominadores iguales. Determinar la suma de las expresiones racionales, $$\frac{3x+5}{3x}+\frac{9x-7}{3x}$$ Solución: sea \(S\) la suma buscada, aplicando el m.c.ds. (m.c.m. de los denominadores) se tiene. \begin{align} &S=\frac{3x+5+9x-7}{3x}\\ &S=\frac{12x-2}{3x}\\ &S=4-\frac{2}{3x}\end{align} Ejemplo 3. Denominadores distintos. Realizar las operaciones combinadas de las expresiones, $$S=\frac{2x-7}{9x^2-2}+\frac{2x+5}{3x+\sqrt2}\left(\frac{2x+1}{3x-\sqrt2}\right)$$ Solución: aplicando el orden de las operaciones, la suma \(S\) está dada por, \begin{align} &S=\frac{2x-7}{9x^2-2}+\frac{\left(2x+5\right)\left(2x+1\right)}{\left(3x+\sqrt2\right)\left(3x-\sqrt2\right)}\\ &S=\frac{2x-7}{9x^2-2}+\frac{2(2x+1)+5(3x+1)}{9x^2-2}\\ &S=\frac{2x-7}{9x^2-2}+\frac{4x+2+15x+5}{9x^2-2}\\ &S=\frac{2x-7}{9x^2-2}+\frac{19x+7}{9x^2-2}=\frac{21x}{9x^2-2}\end{align} Ejemplo 4. Producto de expresiones racionales. Determinar el producto de la expresión, $$P=\frac{2+3x}{3-4x}\left(\frac{3+4x}{3+4x}\right)$$ Solución: note que la fracción entre paréntesis es uno, lo que quiere decir que el producto \(P\) es una fracción equivalente a la primera. Por propiedades del producto de fracciones, se tiene, $$P=\frac{(2+3x)(3+4x)}{(3-4x)(3+4x)}=\frac{6+17x+12x^2}{9-16x^2}$$ Ejemplo 5. Producto de expresiones racionales Realizar el producto de las expresión racional siguientes. $$f(x)=\frac$$

Para más contenidos Ir arriba y luego clic en la pestaña del contenido deseado.

Graficando funciones racionales.

La gráfica de una función racional no posee una forma definida, puede adoptar diversas formas y posee un comportamiento especial en los puntos donde el denominador se hace cero, llamado comportamiento asintótico.

Se dice que una función \(f(x)\) tiene un comportamiento asintótico cuando a medida que la variable independiente x tiende (se aproxima tanto como se desee) a un valor \(c\) escrito como \(x\rightarrow c\) la función \(f\) tiende a infinito (o menos infinito), escrito como \(f\rightarrow\infty,\) esto es, la función \(f\left(x\right)\) tiene un comportamiento asintótico, cuando a medida que x se aproxima (tiende) a un valor, la función crece o decrece sin límite. Dada \(f\left(x\right)\) una función racional de la forma, $$f(x)=\frac{p(x)}{q(x)}=\frac{a_mx^m+a_{m-1}x^{m-1}+\ldots+a_1x^1+a_0}{b_nx^n+b_{n-1}x^{n-1}+\ldots+b_1x^1+b_0}$$ definida para algún intervalo de \(\mathbb{R},\) se puede tener tres tipos de asíntotas lineales, estas son, horizontales, verticales y oblicuas, para la gráfica de \(f(x)\) según sea el caso.

Definición de asíntota vertical

La recta \(x=c\) es una asíntota vertical de la gráfica \(y=(x)\) si y solo si, la función tiende a infinito (o menos infinitos) a medida que \(x\) tiene al valo \(c\) tanto como se quiera por la derecha o por la izquierda.

Las asíntotas verticales si las hay, están en los puntos que hacen cero el denominador, pero no el numerador y dado que para el denominador \(q(x)\) existe un número finitos de puntos \(x=c\) para los cuales \(q(c)=0\) el número de asíntotas verticales para una función racional es finito.

Ejemplo 1. Estudiando la hipérbola. Sin lugar a duda la función racional más estudiada es la hipérbola de dos hojas, que puede ser escrita como, $$f(x)=\frac{c}{x+n}$$ donde \(c\) y \(n\) son elementos de los reales y \(c\neq0.\) 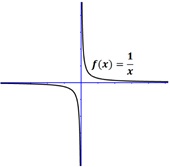En su forma más simple se escribe como, \(f(x)=1/x\) como en la figura de la izquierda donde observa que la recta \(x=0\) es asíntota vertical de la función, esto es \(f\) crece (o decrece) sin límites cuando \(x\) tiende a cero.

Ejemplo 2. Dada la función \(y=\frac{}{2x^3+x-1}{x^2-1} determinar las asíntotas verticales si las hay. Solución: se deben determinar los valores de \(x\) que hacen cero al denominador y no al numerador, para tales puntos la función crece (o decrece) sin límite y por tanto son asíntotas verticales. $$y=\frac{2x^3+x-1}{x^2-1}=\frac{2x^3+x-1}{\left(x+1\right)\left(x-1\right)}$$ Dado que los valores \(x=-1\) y \(x=1\) no hacen cero al numerador, las rectas \(x=-1\) y \(x=1\) son asíntotas verticales.

Ejemplo 3. Determinar las asíntotas verticales de la función racional, $$f\left(x\right)=\frac{x^2-4}{x^3+3x^2-6x-8}$$ Solución: reescribiendo la función en forma factorizada como, $$f\left(x\right)=\frac{\left(x+2\right)\left(x-2\right)}{\left(x+1\right)\left(x+4\right)\left(x-2\right)}=\frac{\left(x+2\right)}{\left(x+1\right)\left(x+4\right)}$$ se concluye que para \(x=-1\) y \(x=-4\) el denominado \({\rm g}(x)=0,\) mientras que el numerador no, por tanto, las rectas \(x=-1\) y \(x=-4\) son asíntotas verticales.

Asíntotas horizontales y oblicuas.
Si para una función racional f cualquiera el numerador y denominador son del mismo grado la función f tiene por asíntota horizontal la recta \(y=a/b\) donde \(a\) y \(b\) son los coeficientes principales del numerador y denominador, además si una función tiene asíntota horizontal no posee asíntota oblicua la cual es la recta \(y=mx+n\) que resulta del cociente de los polinomios que forman a \(f.\)

Ejemplo 4. Dadas la siguiente función, determinar todas las asíntotas. $$y=\frac{5x^3+3x-4}{x^2-3x-4}$$ Solución: resolviendo \(x^2-3x-4=0\Longrightarrow(x-4)(x+1)=0\) de donde las rectas \(x=4\) y \(x=-1\) son asíntotas horizontales, por hacer cero al numerador y no al denominador. Dado que el numerador es un grado mayor que el denominador tiene una asíntota oblicua esta es la recta que resulta ser el cociente de los polinomios \(y=5x.\)

Ejemplo 5. Dada la función racional $$y=\frac{9x^2-7x+11}{3x^2-2x-1}$$ determinar todas las asíntotas.
Solución: como numerador y denominador son del mismo grado la recta \(y=9/3\) esto es \(y=3\) es asíntota horizontal, por tanto, no tiene asíntota oblicua. Las ecuaciones de las asíntotas verticales (si las hay) están dadas por los valores que hacen cero el denominador, pero no al numerador. \begin{align} &y=3x^2-2x-1=0\\ &(x-1)(3x+1)=0\\ &\left\{ \begin{array}{l} x-1=0⟹x=1\\ 3x+1=0⟹x=-1/3 \end{array}\right.\end{align} como estos valores no hacen cero a numerador, las rectas \(x=1\) y \(x=-1/3\) son asíntotas verticales.

Para más contenidos Ir arriba y luego clic en la pestaña del contenido deseado.